Analysis: Notes and Feedback
July 25, 2012
Thanks to everyone who sent feedback on last week's article, "Are We Entering the Age of the Super-Blockbuster?". In this week's notes and feedback column, I share some of the best comments and suggestions, and also note a couple of articles that have popped up online in the last week. While the media and industry seems to be off and running with the "super-blockbuster/uber-hit" idea, our readers point out some ways that we need to do more work to pin down exactly what's going on.
First up, Steven Zeitchik and Amy Kaufman posted an article on super-blockbusters, "As big movies' box office soars, the number of flops rises", which discusses the issue a little more broadly than Mr. Zeitchik's original article. While most people agree with the theory, there's not a lot more than anecdotal evidence presented in the piece. (For more on hard numbers, read on!)
Meanwhile, Jim Pagels at Slate posted "The Dark Knight Rises and the end of counterprogramming: Why Batman had no competition at the box office." This article talks about the steeper weekend-to-weekend drop-offs experienced by films in recent years. I compiled some data on this for Jim that he wasn't able to use in the article in the end (but which I will use myself in another article I'll be posting soon).
It's worth noting that the two central ideas here -- that movies are spending longer at number one, and that movies are declining more quickly at the box office -- are somewhat at odds with one another. If a film is going to lose 60% of its box office in its second weekend, instead of the 50%, or 40% that it would have declined five or ten years ago, then the chances it will stay at number one would seem to diminish. So if films are declining faster, but still lasting longer at the top of the chart, they are perhaps doing extra well in comparison to other films coming out in subsequent weeks.
There are other explanations though. First, as pointed out by Frank Geilenkirchen in an email,
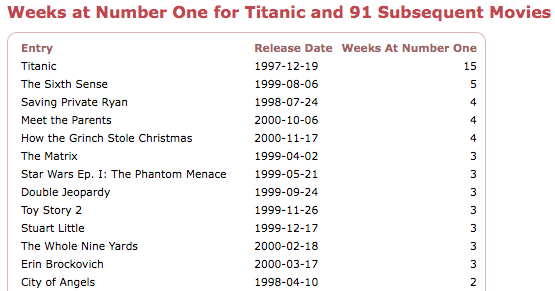
I did try to address this problem in the article by using a 100-movie sample, although that doesn't completely get around the problem that we might be looking at an anomaly. Following Frank's suggestion, we can compile the list of weeks at number one for Titanic and the 91 films that followed it at the top of the chart. The chart can be found here, and downloaded as CSV here. Here are the first few lines
Erik Gunther adds another suggestion:
Another reader noted that several other factors may be at play, including studios getting better at timing releases of films, for example by releasing major films in early May instead of waiting until Memorial Day. And, along similar lines, smaller films might be moving out of the Summer into quieter times of the year, like April and October.
So the super-blockbuster remains an elusive beast for now. There's a tantalizing glimpse that there's something there, but we need to do some more work to determine what, if anything, is going on. I'll have some analysis of another piece of the puzzle in my next article... coming soon, as they say.
As always, I welcome your feedback and comments, and if you see an interesting article online that you think is worth sharing, please let me know.
Bruce Nash - bruce.nash@the-numbers.com
[A]ren't we falsifying our findings by starting the observation with the blockbuster of the decade? My question is: Would a t-test show a significant result, if we compared the 92-movie-period which started with Avatar to the 92-movie-period which started with Titanic? Results would be more apples-to-apples because they both include the decade's major success.
 Factors like the increasing reliance on movie franchises and the consequent lack of original material play a role as well (more sequels = more surefire hits). Haven't I read, that the overall number of new releases has been relatively low in the past 1-2 years as well? No wonder then, that released films have more staying power.
Factors like the increasing reliance on movie franchises and the consequent lack of original material play a role as well (more sequels = more surefire hits). Haven't I read, that the overall number of new releases has been relatively low in the past 1-2 years as well? No wonder then, that released films have more staying power.
Reading your article made me think of some of the network effects that occur in business. I believe the concept is described in Christensen's Innovator's Solution, Web 2.0: A Strategy Guide, or maybe Crossing the Chasm. Sorry, but I don't recall which one. The idea is that consumers vote for a single dominant winner since there is value in everyone using the same technology. For example, in order for a telephone to work, there needs to be someone on the other end. So consumers instinctively drive to a single technology. Obviously movies are very different. It doesn't matter that one dominates over another, but I can't help but feel there's something similar going on here. It's like people want to elect a movie as the big winner because it enhances their enjoyment and customer experience.
Filed under: Analysis


